TYT Matematik Deneme PDF
PDF İndirmek için tıklayınız.
Video çözümlü TYT Matematik Denememizin Kapağı.

Sınav Ambiyansını yaşayın.


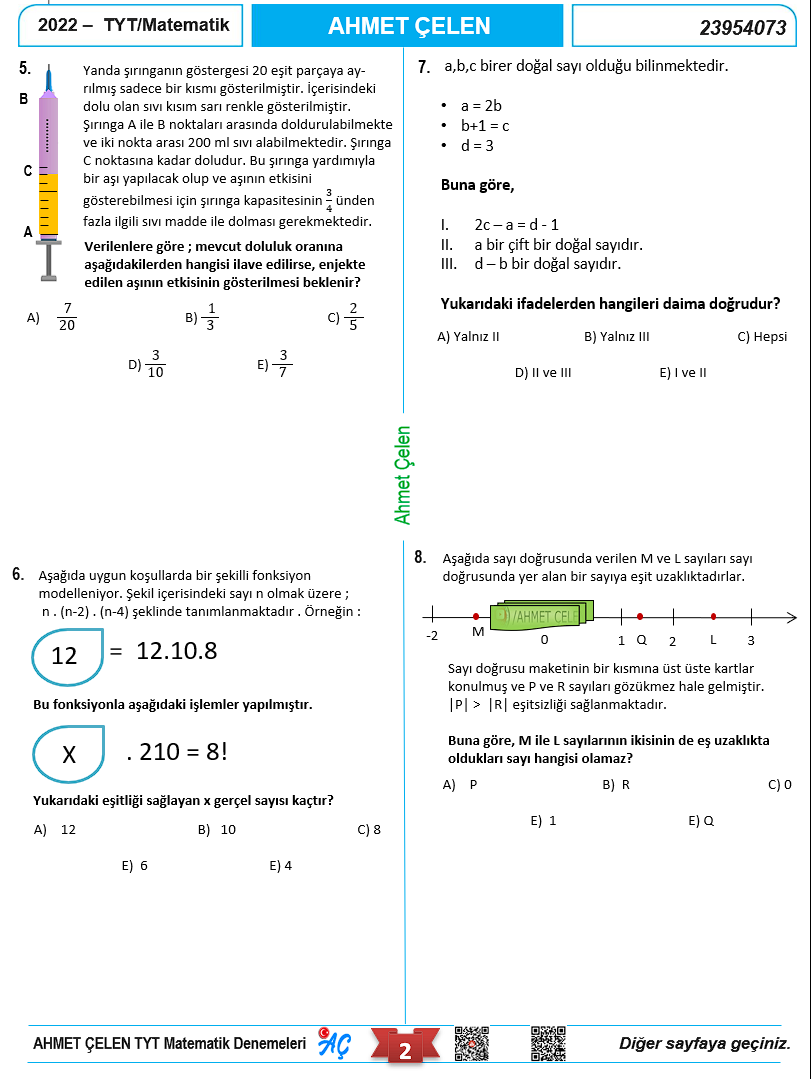


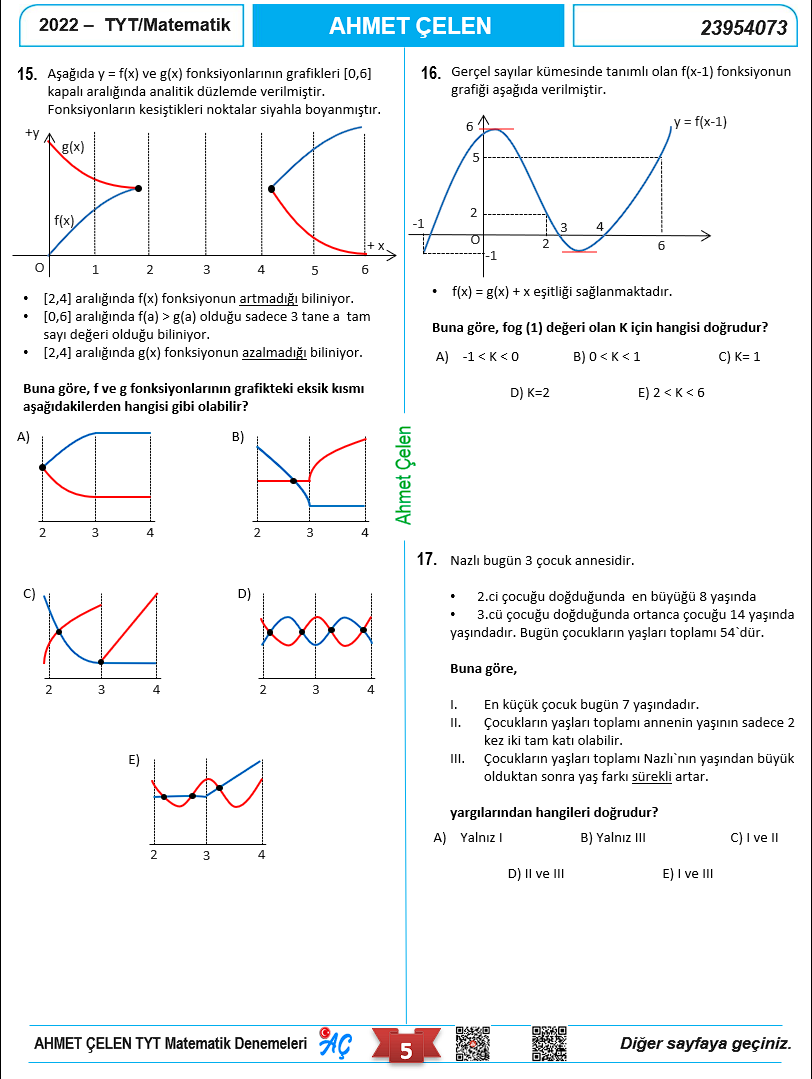
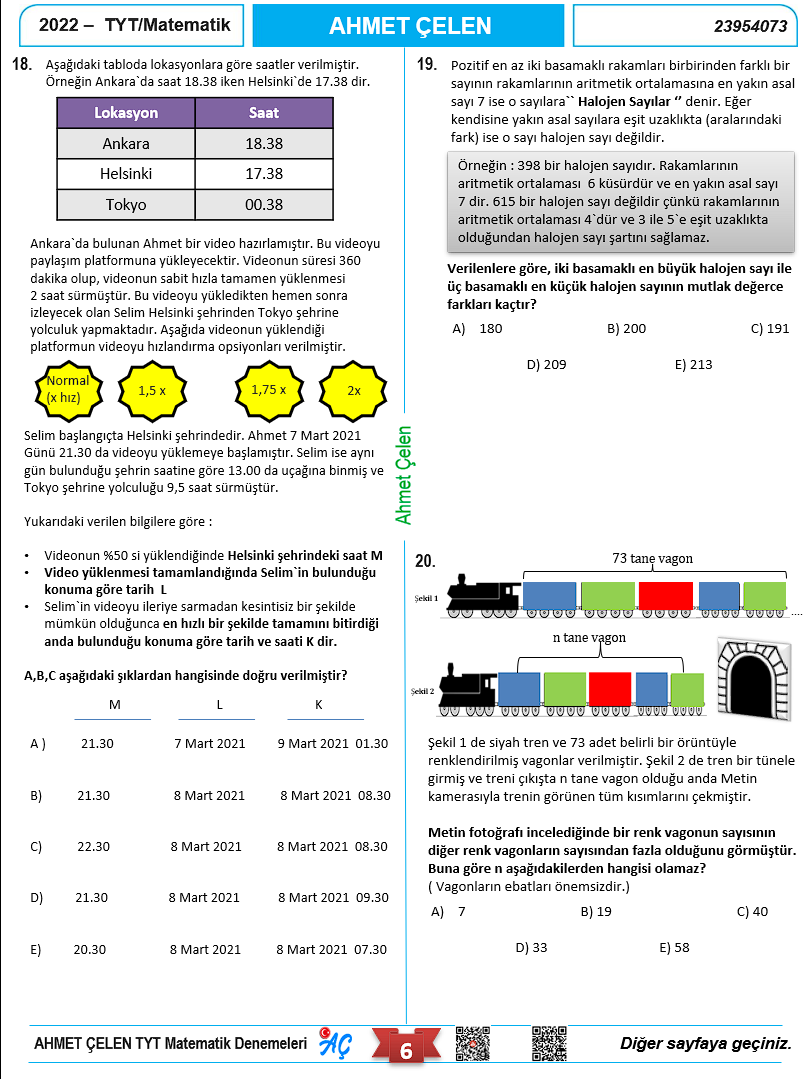
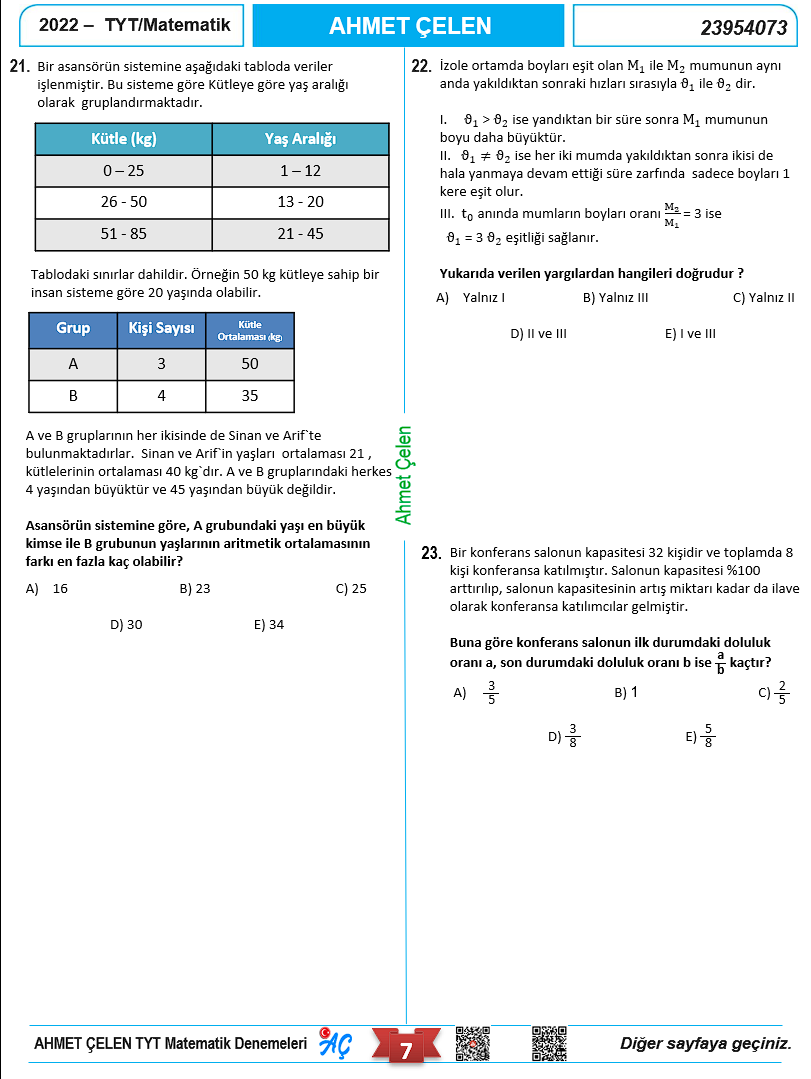
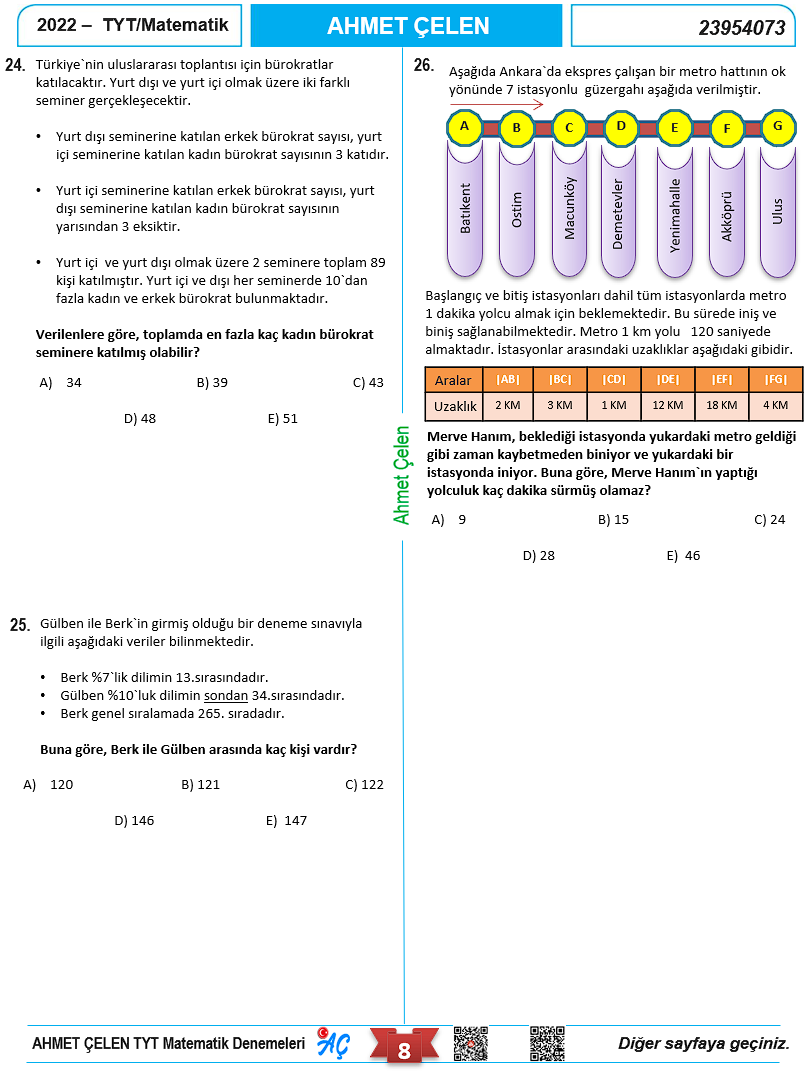
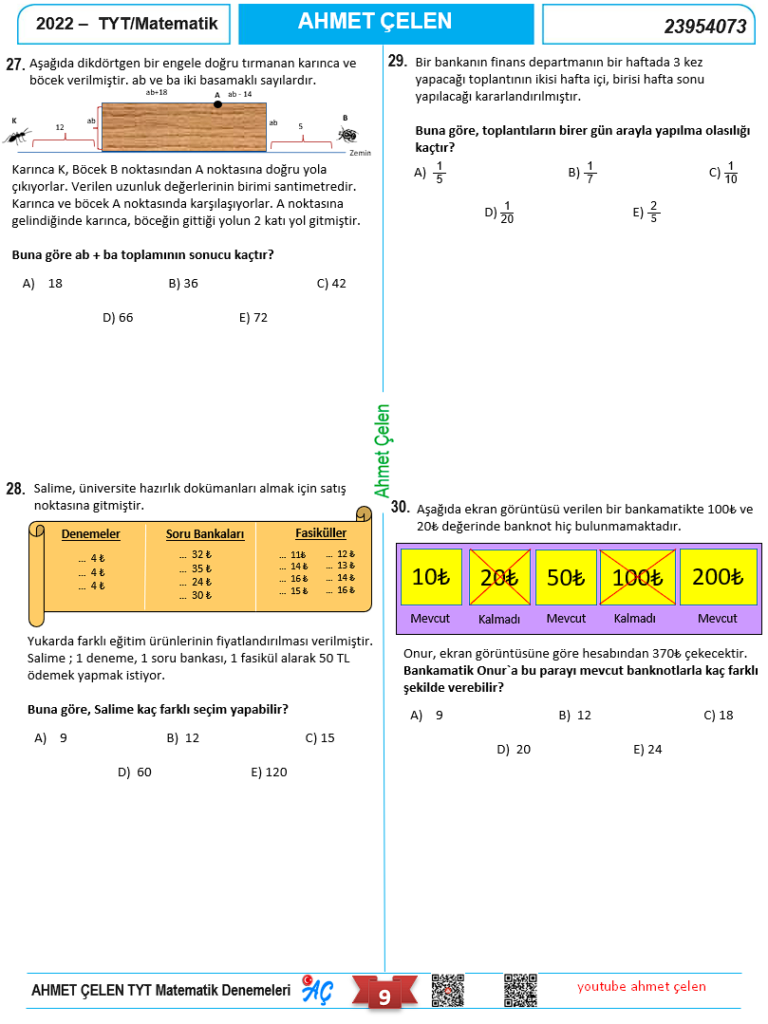


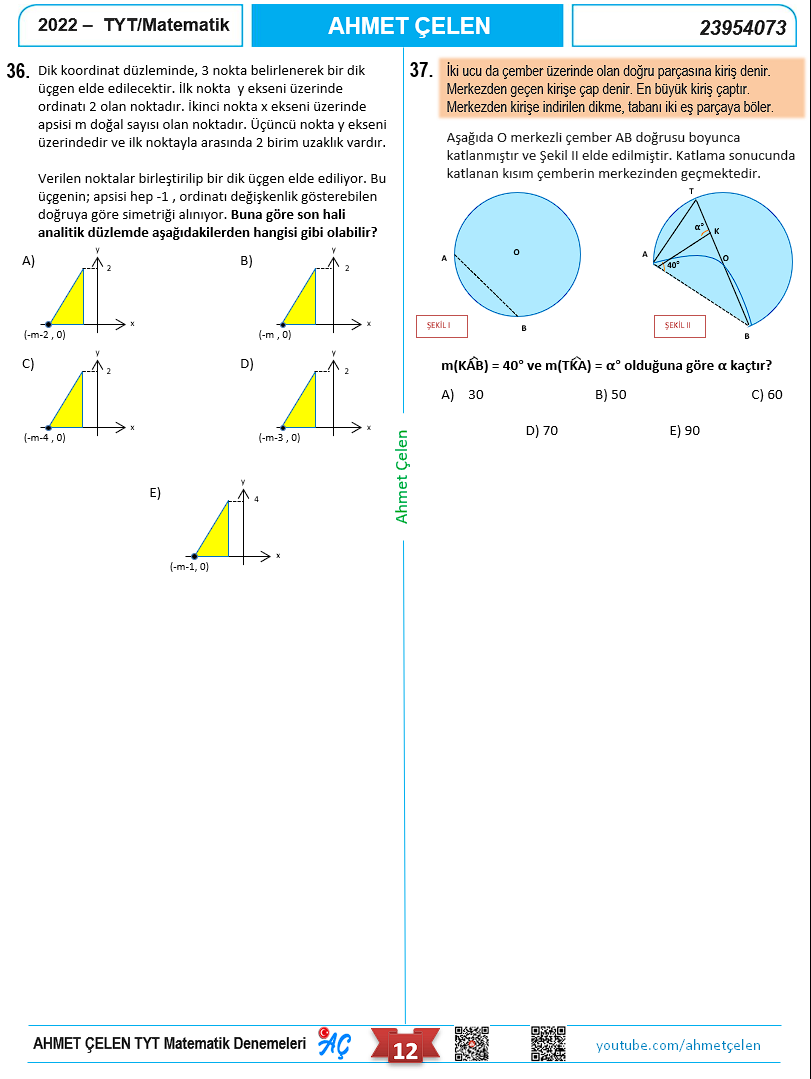
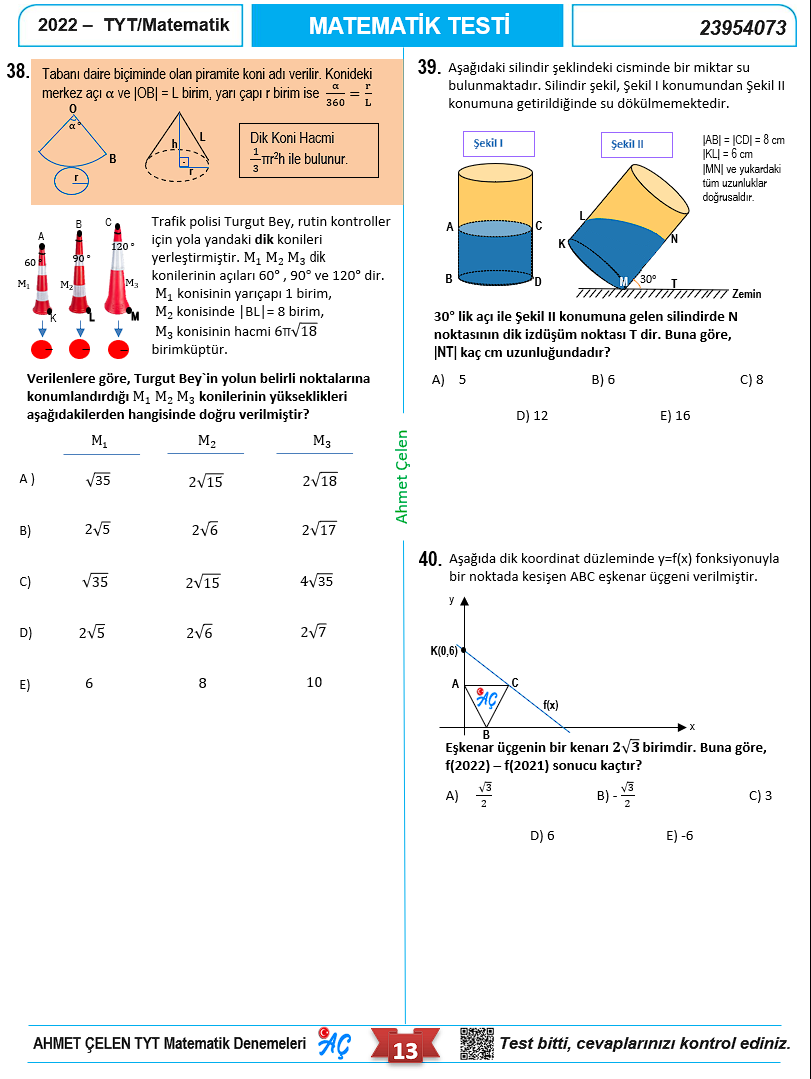

Video çözümlü TYT Matematik Denememizin Kapağı.

Sınav Ambiyansını yaşayın.




















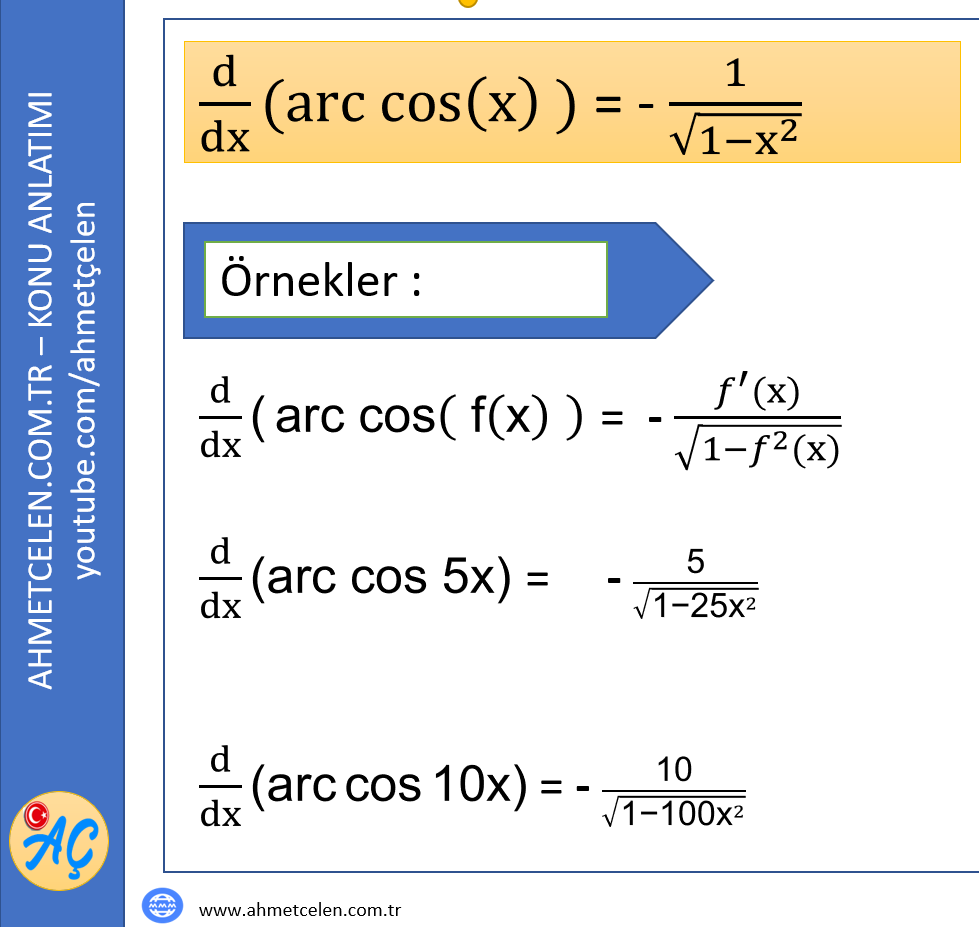
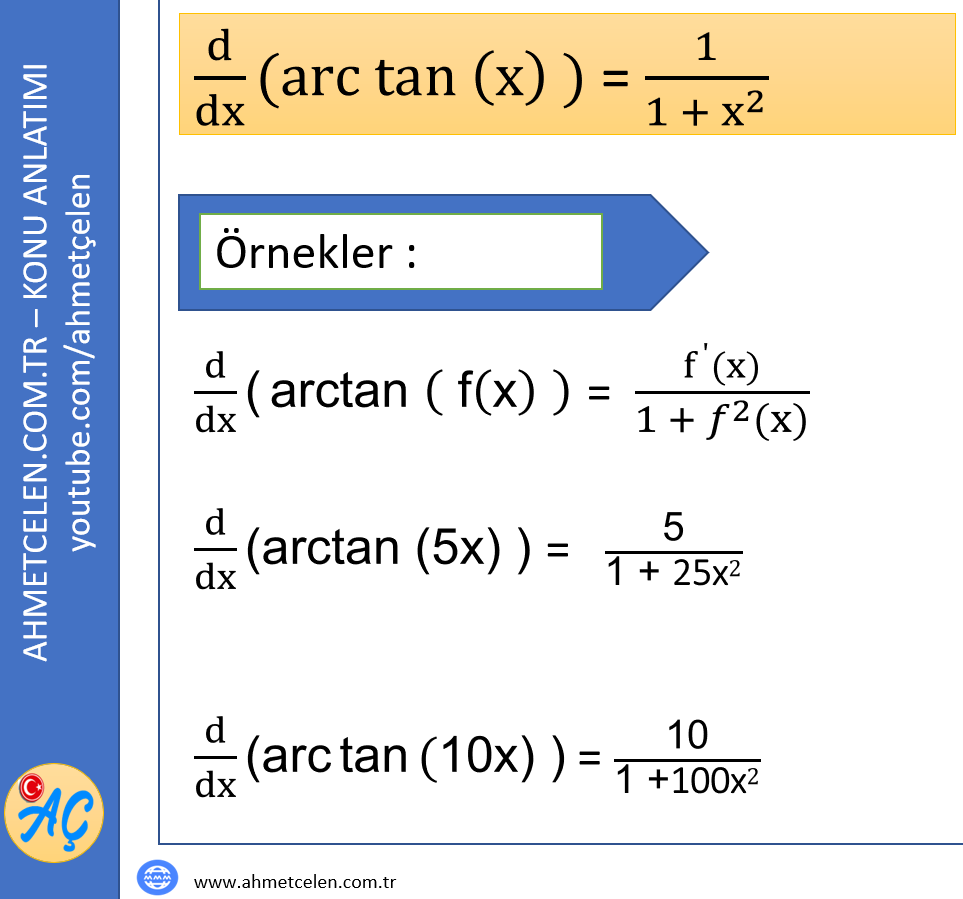

Yukardaki bağlantıya tıklayarak Çemberin Analitiği Konu Anlatımı PDF indirebilirsiniz.
Bir düzlemde sabit bir noktaya eş uzaklıkta bulunan noktaların kümesinin oluşturduğu geometri şekle çember adı verilir. Çemberin içi boş bir yuvarlaktır. Daireden farkı içi boş olduğundan ötürü alanının hesaplanamamasıdır.

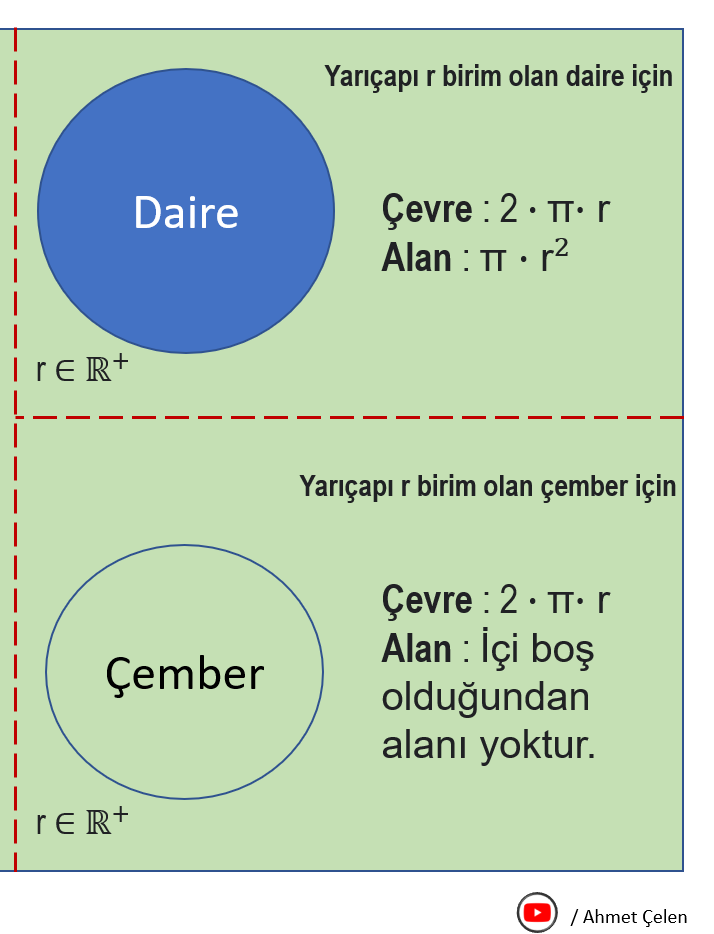




Merkezi orijin ve yarıçapı 1 birim olan çembere “Birim Çember” denilir.

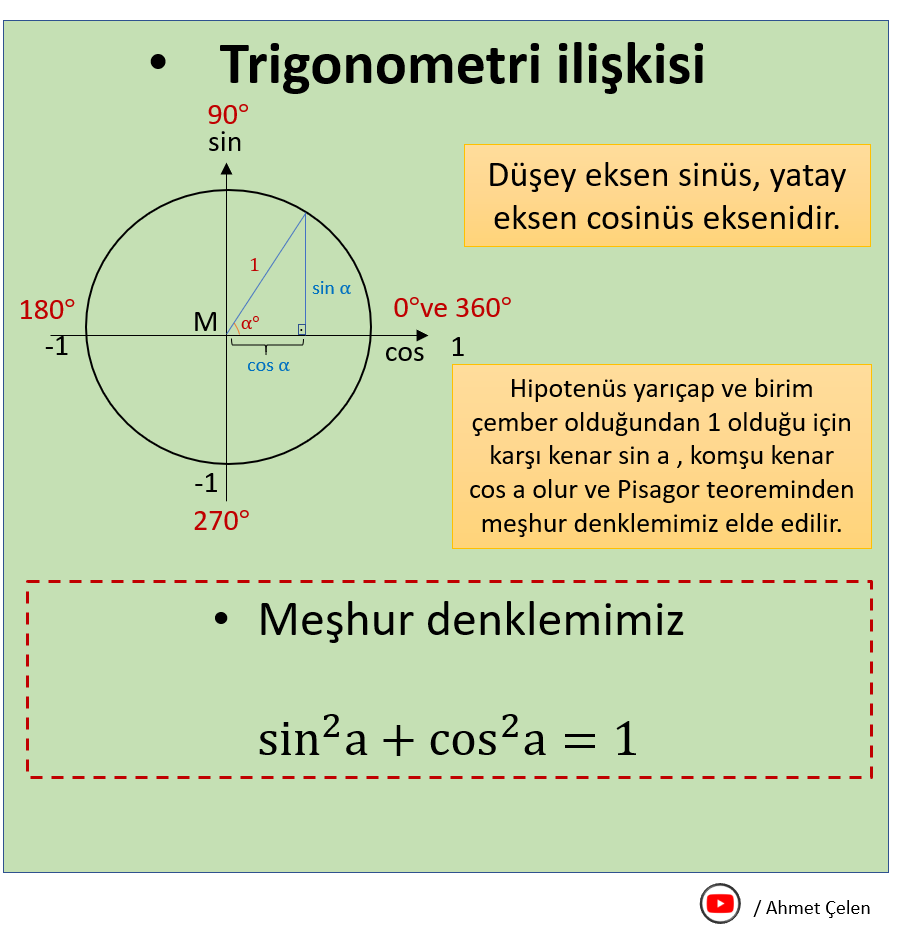








Aşağıdaki soruların çözümleri için konu anlatımı bittikten sonra uğraşmanızı tavsiye ediyoruz. Uğraştıktan sonra yapamazsanız çözümünü de paylaştık bakabilirsiniz. Bu şekilde yapmanız sizi daha çok geliştirecektir.


Çemberin analitik incelenmesi 12.sınıfın II.dönem son konularından bir tanesidir. Lise matematik adına güncel müfredatta geometri için işlenilen en son konudur.
11.Sınıf ve 12.sınıf konuları AYT (Alan Yeterlilik Testi) , 9. ve 10.sınıf konuları ise TYT (Temel Yeterlilik Testi Konusudur. İstisnalar olabilmekte ve ortak olarak bazı konular her iki sınavda da yer alabilmektedir. Çemberin analitiği 12.sınıf konusudur ve alan bilgisi gerektirdiğinden AYT sınavına dahildir. TYT sınavında çemberin analitiği sorusu müfredat göze alındığında sorulamaz. Çemberin analitiği 12.sınıfın konusu olduğundan ötürü AYT Matematik kısmında son derecede önemli bir yere sahiptir. 12.Sınıf konuları AYT matematik sınavında bir hayli fazla soru kontenjanına sahip konulardır. İntegrla ile harmanlanarak bir çok soru kalıbı sınavda orta ve zor olarak yer alabilmektedir.

Logaritma Konu Anlatımı PDF yazımız için aşağıdaki bağlantıya tıklayarak PDF indirebilirsiniz.
Logaritma Fonksiyonu :
Şimdi detaylıca logaritma fonksiyonu ele alalım. Özellikler en alttadır.



Logaritma fonksiyonu bir çok bilim dalında kullanılmaktadır. Fizik, kimya, biyoloji, doğa bilimleri, astronomi gibi daha çok fen bilimleri tarafınca kullanılmaktadır. Ekonomik durumlarda da üstel fonksiyonla birlikte kullanılabilmektedir. En yaygın ve popüler kullanım alanlarını derleyelim.
John Napier (1550-1617) : Logaritmayı Bulan İskoçyalı matematikçidir.
Gelenbevi İsmail Efendi (1730 – 1790) : Logaritma cetveli hakkında çalışmış ve zamanında rehberlik etmiş eserler vermiştir.
Şimdi Konu Anlatımımıza devam edelim.






Logaritma Özellikleri Büyük Foto :
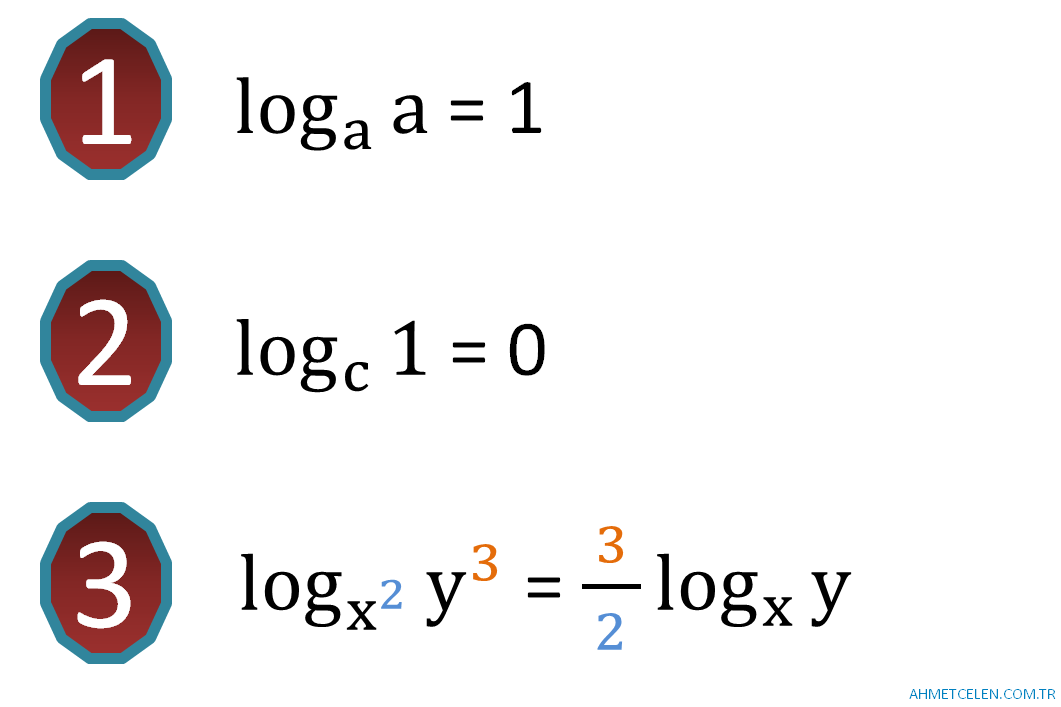

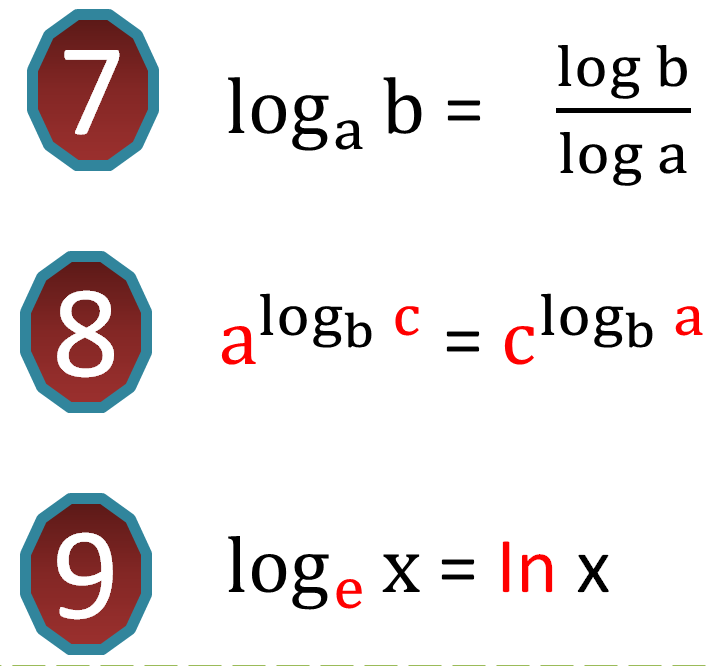
Logaritma 12.Sınıf AYT Matematik konularının başlangıcıdır. 12.Sınıf konusu olması AYT Matematikte büyük rol oynadığını göstermektedir. Diğer konulara nazaran zevkli ve öğrenilmesi biraz daha kolay bir konudur. AYT Matematik sınavında her sene düzenli olarak soru gelmektedir. Ortalama 2-3 soru sorulmaktadır ve sorular çok zor gelmemektedir. Logaritma taraflı henüz çok zor bir soru gelmemiştir. Fakat şunuda unutmayın ki her konudan her türlü zorlukta soru gelebilir.
Logaritma görüldüğü üzere üstel fonksiyonun tersidir. Dolayısıyla üstel fonksiyon ve üslü sayı bilgilerimizi bir hayli kullanmaktayız. Ayrıca köklü sayılarla da sorularda çok karşılaşılmaktadır. Onlara da hakim olmakta fayda var. Logaritmanın ilerki konular olan limit türev integralle güncel müfredat olarak doğrudan bir ilişkisi bulunmuyor.
YouTube Kanalıma abone olarak ücretsiz videoları izleyebilir PDF` leri ücretsiz indirebilirsiniz. Link aşağıda.
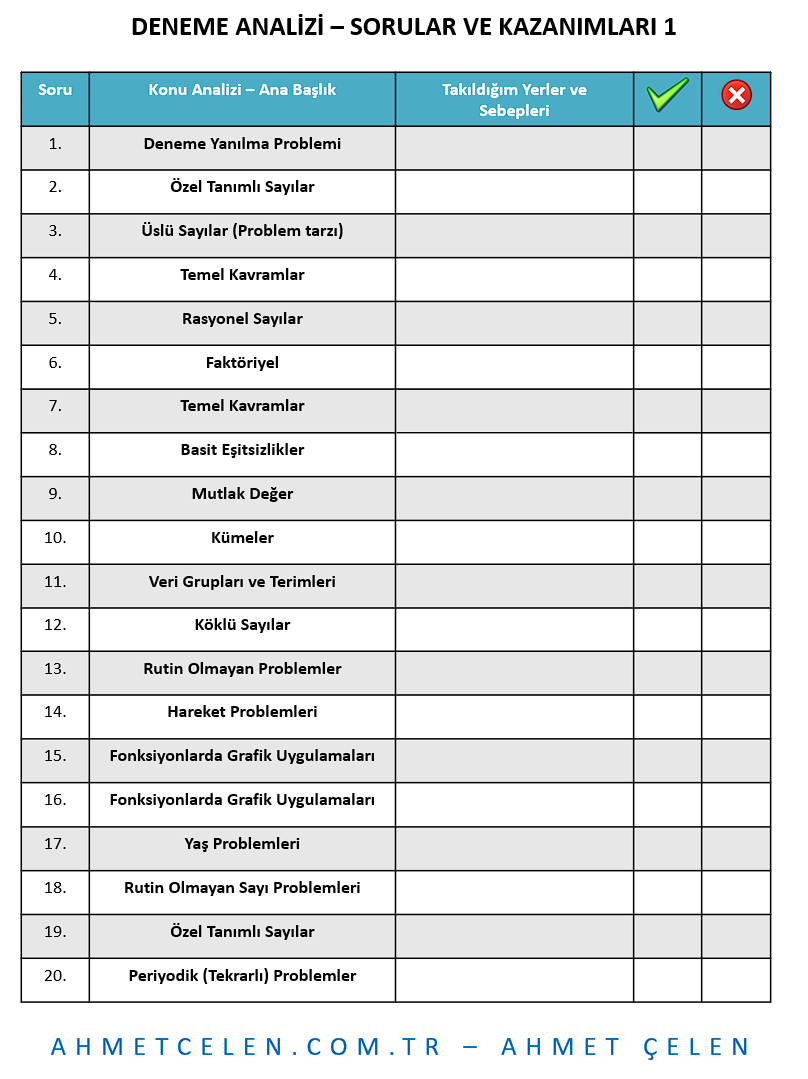
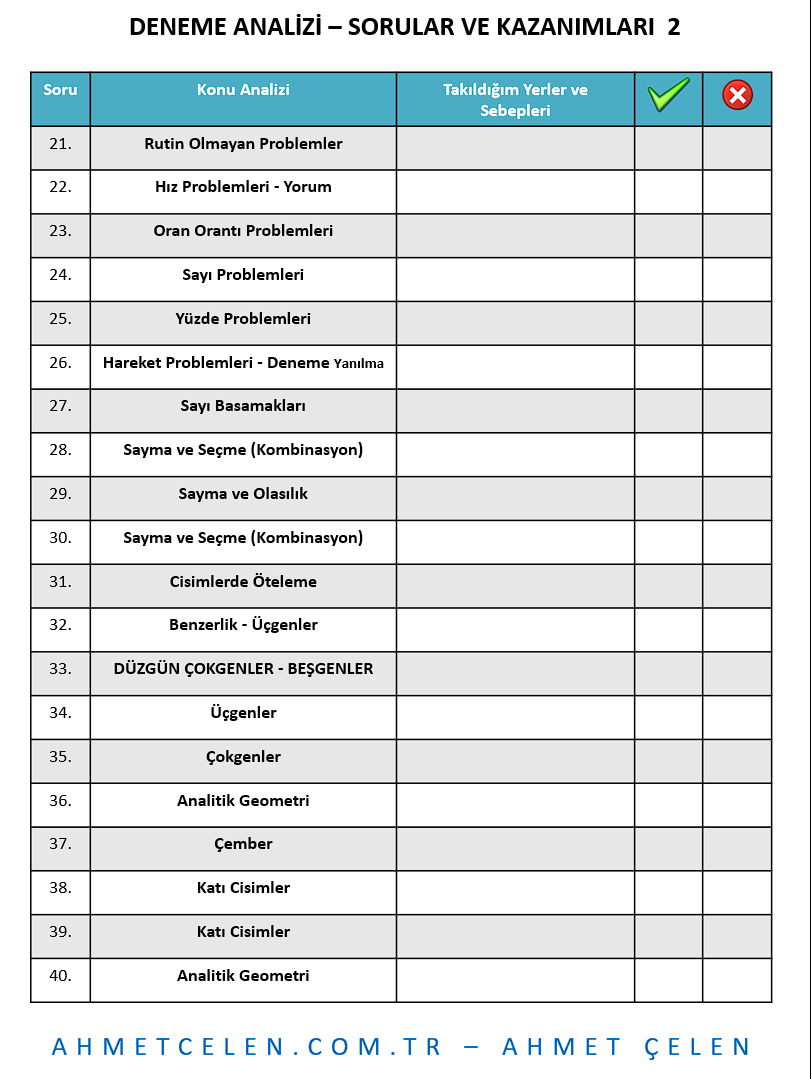
Aşağıdaki videomuzu izlerseniz yanıt bulacağınız sorular ve kazanımlarınız.
Ezbere değil, mantığa dayalı bir anlatım eşliğinde 40 dakikada logaritmayı öğrenin. YouTube platformunda daha rahat izleyebilirsiniz. Buna benzer video ve içerikler için abone olmayı unutmayın.

Karmaşık sayılar PDF Test Konu Anlatımı başlığımız adı altında önce bir karmaşık sayıların tanımını verelim. Karmaşık sayıların çıkışı bir sayının karesinin negatif olmasından ötürü çıkmıştır. Bu sayı i diye tanımlanmış ve karesi -1 olarak kabul edilmektedir. Aşağıdaki linke tıklayarak PDF testimizi indirebilirsiniz.
Aşağıdaki linke tıklayarak PDF testinizi indirebilirsiniz. Faydalı olmasını diliyorum.
AHMET ÇELEN









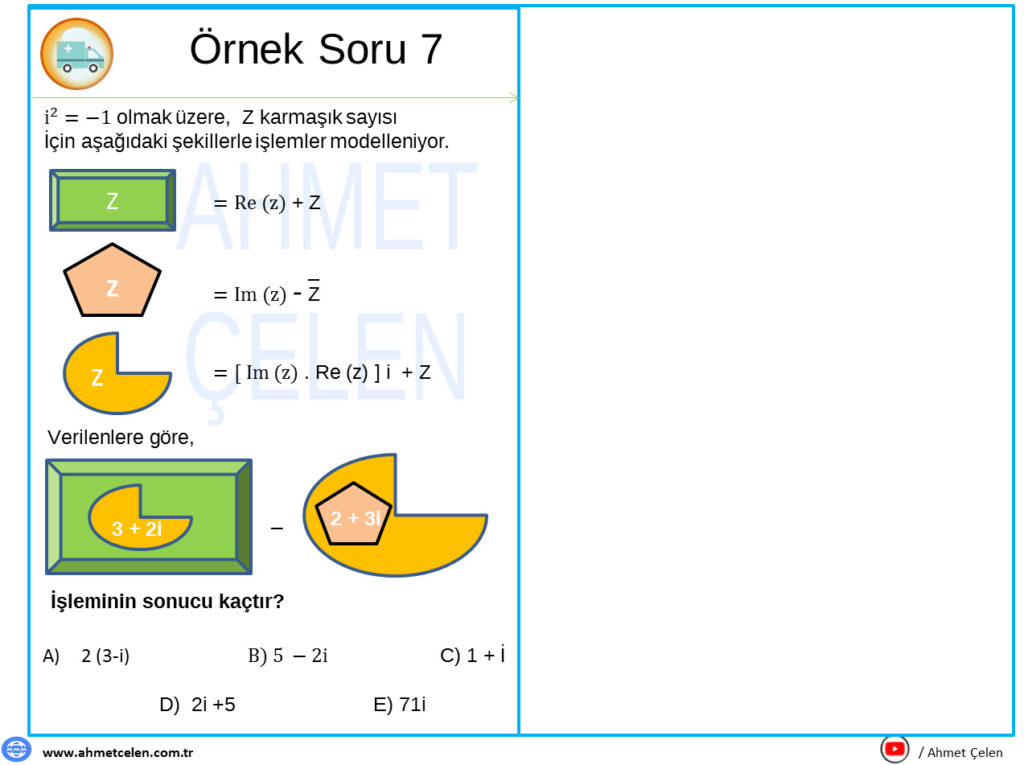






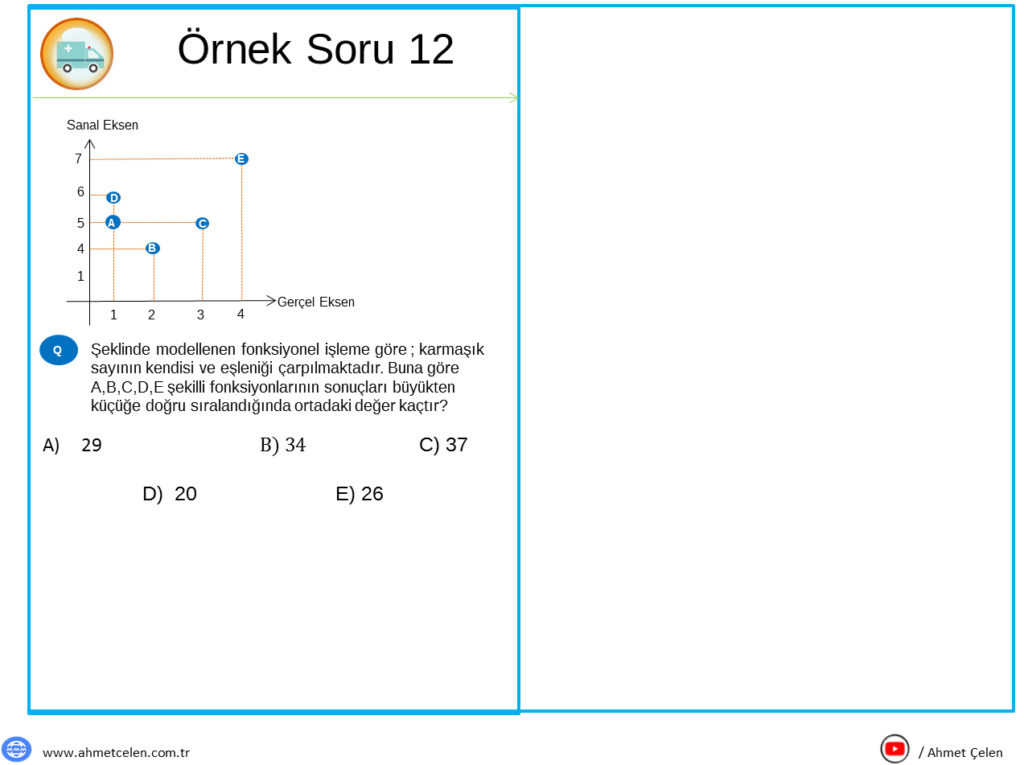



Yukarıda paylaştığımız soruların çözümleri video halinde YouTube Ahmet Çelen Kanalındadır, isterseniz bakabilirsiniz.
_______________________________________________________________
Karmaşık sayılar eskisi gibi zor ve uzun müfredat içeren bir konu değil. Yeni değişen sınav sistemi (AYT) ile birlikte soruların daha kısa ve geçmiş yıllara nazaran daha kolay geldiğini söyleyebilmekteyiz. Ayrıca müfredat olarak karmaşık sayılarda büyük bir daraltma yapıldı. Sadece temel kısımlar kaldı. Dolayısıyla bu durumda öğrencilerin lehine bir durumdur. Karmaşık sayılar ayt matematikte kolayca net kazanabilinecek konulardandır. Her yıl yeni sınav sistemi ÖSYM AYT sınavında düzenli olarak soru sormaktadır . Soru sayısı ortalama olarak 1 ve 2 olarak görülmektedir. Önümüzdeki seneler içinde bu rakam çok değişmeyecek gibi durmaktadır.
Yazımızda paylaştığımız Karmaşık sayılar Test Konu Anlatımı PDF dosyasında yer alan sorular çıkmış sorular analiz edilerek ve çıkması muhtemel sorular için tahminler yürütülerek beceri temelli her zorlukta soru hazırlanmıştır. Soru sayısının az olmasında karşın konuyu güzel bir şekilde özetleyen nitelikli sorulardan oluşmaktadır.
Karmaşık sayılar, diğer konularla doğrudan çok büyük bir ilişkisi ve temel gereksinimi olmadığını söyleyebiliriz. Örneğin üslü sayılar ve logaritma gibi çok bağdaştırılabilir bir durum yoktur fakat hiç de olmadığını söyleyebilmekteyiz. Fakat ikinci dereceden denklemlerle bağdaştığını ve konuya hakim olmak adına bilinmesi gereken iki konudur. İkinci dereceden denklemlerde gerçel kök bulunmadığı takdirde bu köklerin imajiner kökler olduğunu söyleyebilmekteyiz artık.

Tek ve Çift Fonksiyonlar Konu Anlatımı PDF olarak ücretsiz bir şekilde sizlere sunacağız. Aşağıda kırmızı bağlantıya tıklayarak indirebilirsiniz.
Faydalı olmasını diliyorum. ~ Ahmet ÇELEN
Yukarıda çift ve tek fonksiyonların özetini kısaca aktardık biraz detay bilgi isteyenler için görseller yardımıyla değerlendirelim.



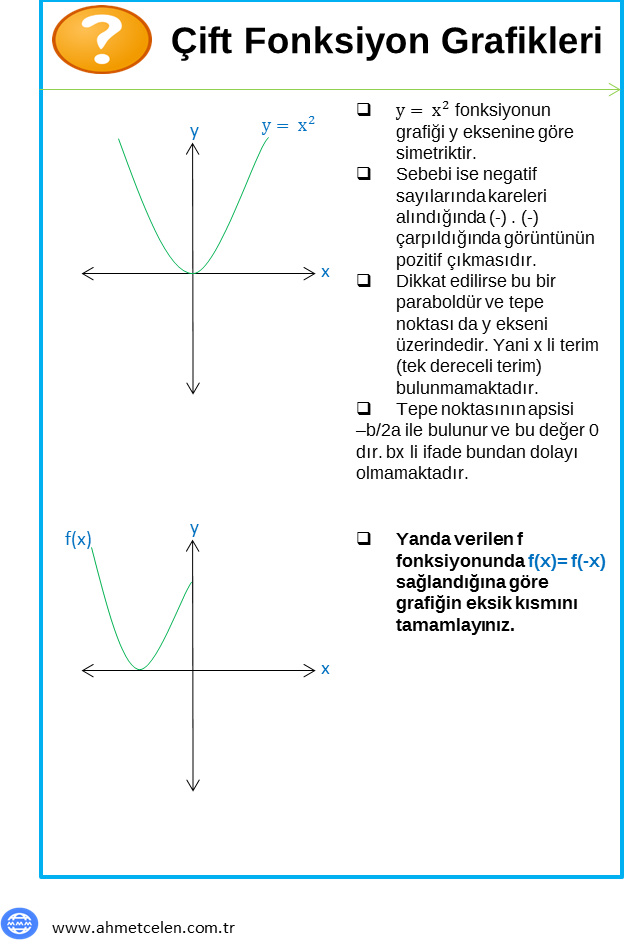

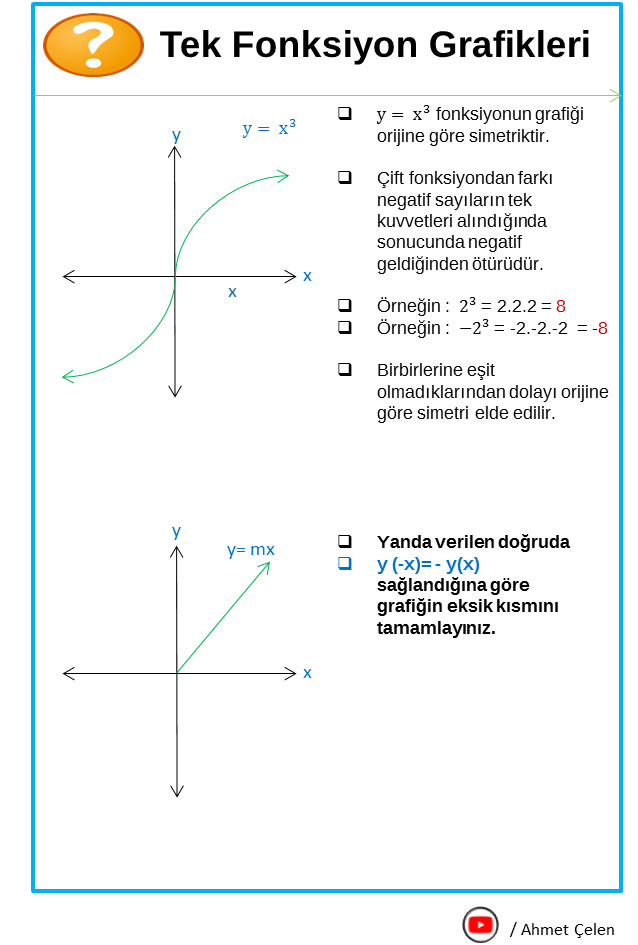









Arkadaşlar bu soruların çözümlerini video olacak şekilde YouTube kanalımda çözdüm. Aşağıdan soruların çözümü ve genel olarak videolu konu anlatımı izleyebilirsiniz. Videoyu yazıma aşağıya entegre edeceğim.
Fonksiyonlar matematiğin yapı taşıdır. En temel bilgiler ve diğer konuların temelidir. Fonksiyonları bu sebeple çok sağlam tutmalıyız. İlerleyen konularda limit türev integral gibi ağır konularda fonksiyon temelimiz iyi olursa zorluk çekmeyiz. Ayrıca bazı özel fonksiyonların grafiklerini çizebilmemiz ve nasıl olduğunu bilmemizde büyük kolaylık sağlar.
X2 , X3kök içerisinde x , In x gibi karşımıza çok çıkacak fonksiyonların grafiklerini bilirsek eşitsizlik ve kök (kaç noktada kesişir) gibi sorularında grafikten hiç işlem yapılmaksızın tespit edilebilir ve cevaba ulaşmış oluruz. Özet olarak fonksiyonlar hem TYT hem AYT matematik için büyük önem taşımaktadır. Ayrıca çarpanlara ayırma da matematiğin temelidir ikisini iyi bilirseniz sorularda her konuda olursa olsun çok zorlanmazsınız.

Merhaba değerli öğrenciler ve öğretmenlerim. YouTube kanalımda videolarda kullandığım dersi takip ve birebir ilerleme için videolarda kullanılan ders notları ve soruların tamamını bir sayfada yayımlamak istedim. Amacımız kolaylık olsun her videonun altında veya başka yerlerde pdf notu aramaya ihtiyacınız olmasın diye bu sayfayı açmayı uygun gördüm.
Özet olarak bu yazımızda YouTube Ahmet Çelen Matematik kanalının Video Ders Notları bulunmaktadır.

YouTube Kanalıma direkt ulaşmak için tıklayın!
Aşağıda ilgili konu ve tanıtım amaçlı görseller paylaşılmıştır. Dokümanına ulaşmak istediğiniz ilgili konunun ilgili numarasına tıkladığınızda otomatik olarak dokümana yönlendirileceksiniz. Problem yaşamanız halinde bilgi@ahmetcelen.com.tr adresinden bana ulaşabilirsiniz. Videolar yüklendikten sonra buradan da gerekli güncellemeyi sağlamış olacağız. Yeni video yüklendiğinde video ders notları da aynı şekilde sayfa üzerinde güncellenecek farklı bir sayfaya ulaşmanız gerekmeyecektir. Kanalda yaptığımız soru çözümlerinin pdf olarak paylaşmıyoruz isterseniz ekran görüntüsü alarak çıktı alırsınız.
Aşağıda ilgili konunun içerikleri yer almaktadır. Sol tarafta ilgili konunun üstüne tıklayarak otomatik olarak cihazınıza ders notunu indirebilirsiniz. Sağ tarafında ise ilgili konu ve videonun içeriği hakkında kısaca açıklamalar yapılmıştır.
DENEMELER TYT VE AYT :

Son Prova TYT Matematik Denemesini indirmek için tıklayınız!

Parabol Fasikülü indirmek için tıklayınız.
_________________________________

1.Video Parabol Ders Notları : Parabol Giriş Temel Bilgiler
2.Video Parabol Ders Notları : Tepe Noktası ve Simetri Ekseni
3.Video Parabol Ders Notları : Parabol ile Doğru Ortak Çözümü ve Delta
4.Video Parabol Ders Notları : Genel Tekrar Karma Soru Çözümü
5.Video Parabol Ders Notları : Yeni Nesil Beceri Temelli Soru Çözümü
Parabol Zor Sorular : 6. 7. 8. Soru Çözüm Video Ders Notları
______________________________________________________________________

1.Video Türev Ders Notları : Türevin Limit Kullanarak Tanımları
2.Video Türev Ders Notları : Türev Tanjant Eğim İlişkisi ve Uygulama
3.Video Türev Ders Notları : Toplam ve Fark Durumundaki Polinom Fonksiyonların ve X ^ n formatındaki fonksiyonların türevi
4.Video Türev Ders Notları : Çarpım ve Bölümün Türevi
L-Hospital Kuralı Ders Notları : L-Hospital Kuralı ve Örnekleri
______________________________________________________________________

Tek ve Çift Fonksiyonlar Video Ders Notları : Tek ve Çift Fonksiyonlar Full
______________________________________________________________________

Karmaşık Sayılar Tek Video – Ders Notları : Karmaşık Sayılar Tüm Soru Çeşitleri
___________________________________________________________

Logaritma Tanımı ve Tüm Özellikleri PDF : Logaritma Tanımı ve Tüm Özellikleri Video Ders Notu

İkinci dereceden fonksiyonların özelleştirilmiş isimleri Paraboldür.. Aynı zamanda müfredat olarak ikinci dereceden fonksiyon grafik uygulamaları diye de geçer. Parabol Konu Anlatımlı PDF başlığımızda konunun özetini sizlere PDF eşliğinde sunacağız. Her sene ÖSYM 1 tane parabol sorusu sormaktadır. Video çözümlü olarak sizlerde parabol için hazırladığımız fasikülü öğretmen veya öğrenci olarak incelemenizi tavsiye ederiz. İyi çalışmalar.
Aşağıdan isterseniz YouTube üzerinden video şeklinde müfredata uygun konu anlatımlarıma bakabilirsiniz. İstersenizde özet olarak makalemizi okumaya devam edebilirsiniz. Video konu anlatımları için tıklayın.



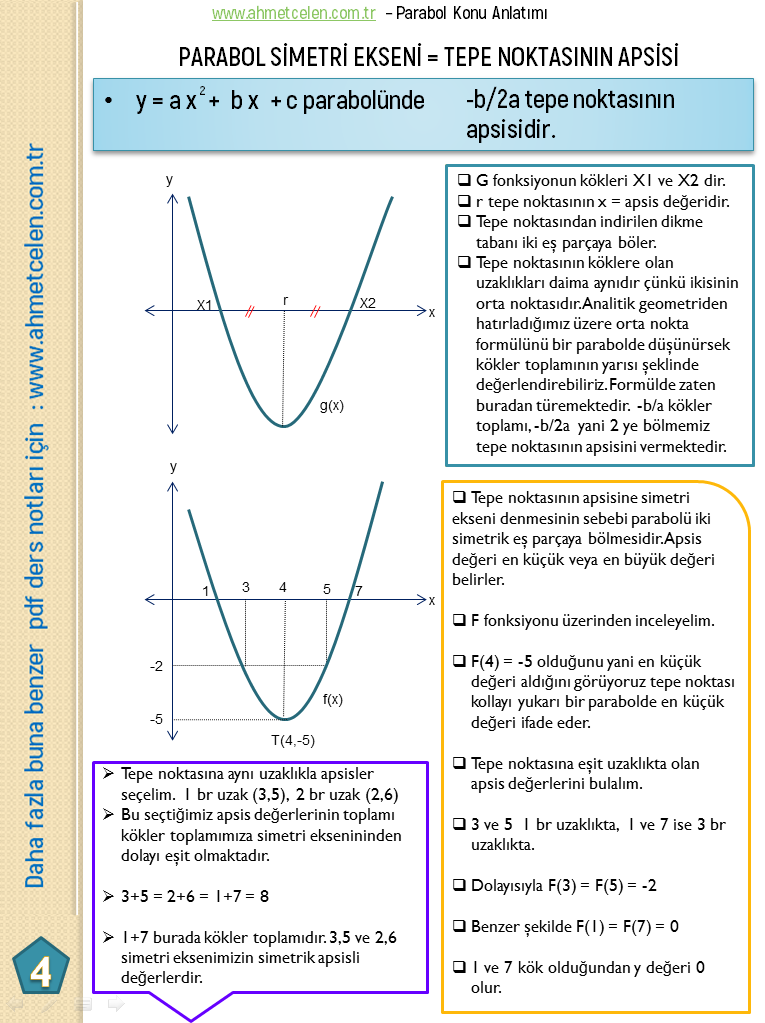
Parabol sorularında genelde 2 farklı şekilde denklem yazmamız istenir.

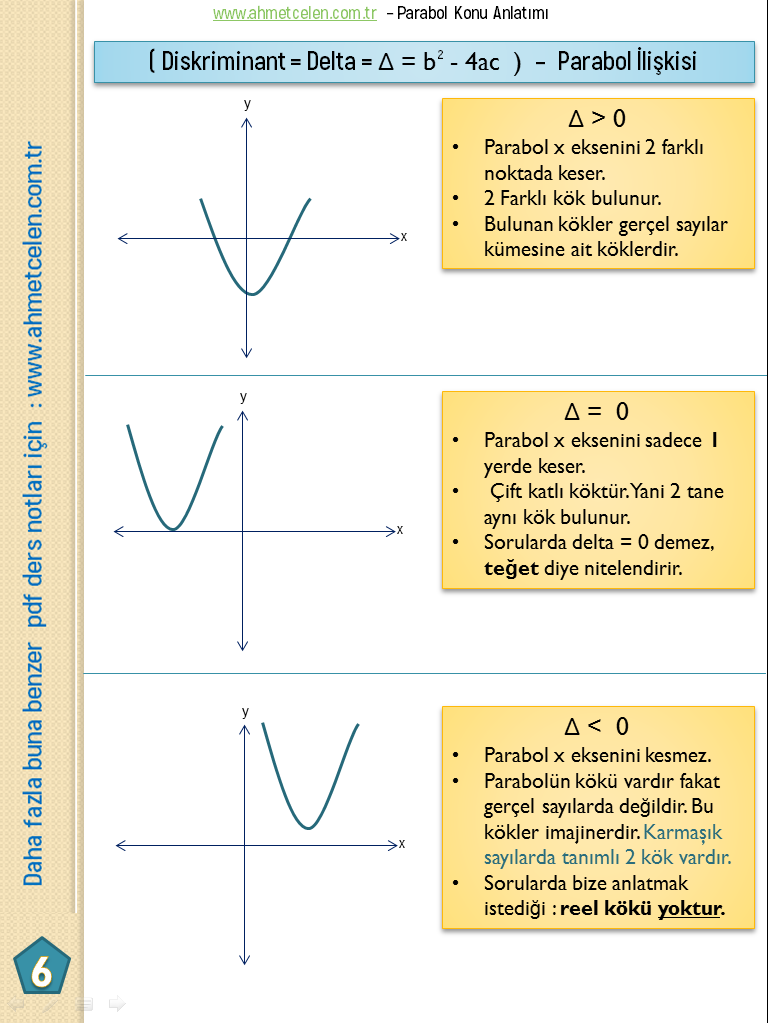


Arkadaşlar bu kısımda lütfen ezberden kaçının. Birbirlerini eşitleyerek denklem çözme olarak soru algınızı değiştirebilirsiniz. Doğru denklemleri konu anlatımdaki gibi olmayabilir – ise + diye geçer mesela o yüzden ezber değil denklem çözme mantığını kullanın burada bilmeniz gereken şey parabol ile doğru ortak çözüm yapılırken tüm ifadeler bir tarafta toplanır ve soruda verilenlere göre diskriminant incelemesi yapılır.

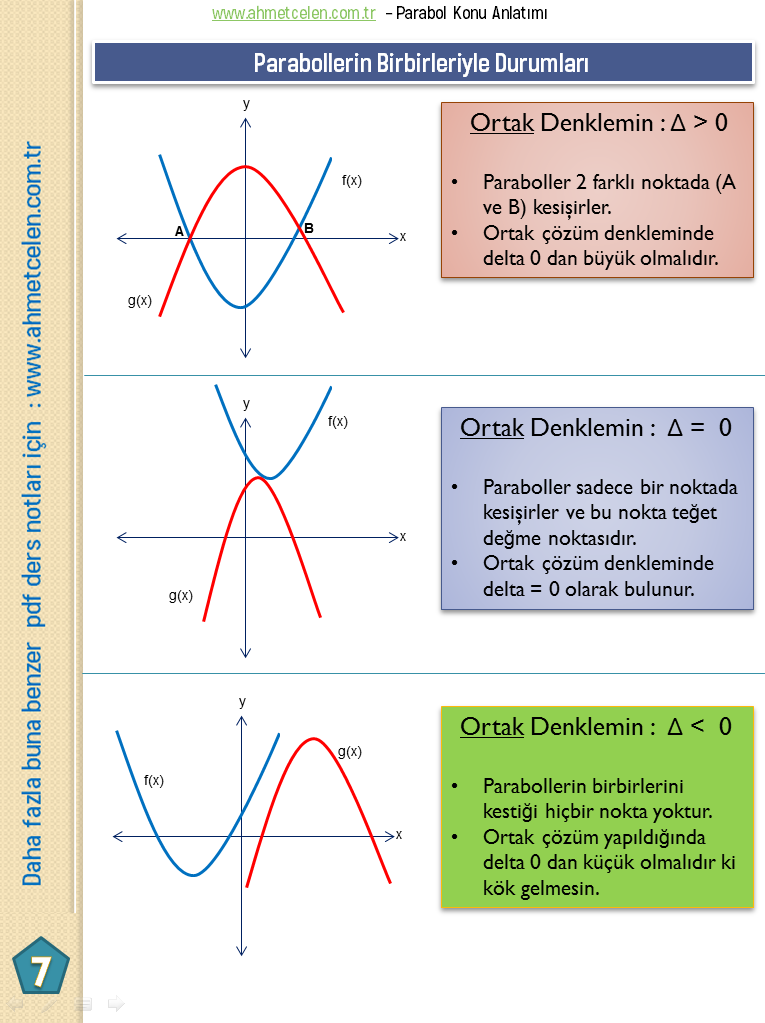
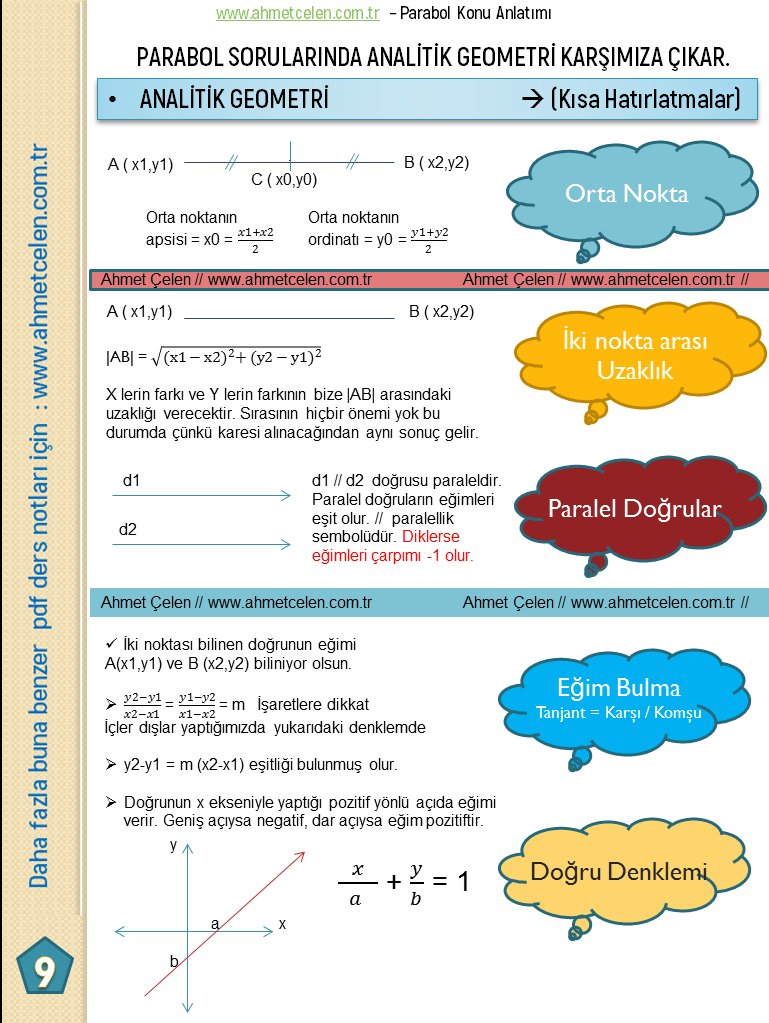


Her kaynakta hemen hemen yer verilmeyen bazı unutulan bilgileride ekleme gereği duyduk. Alan Yeterlilik Testi bilgi isteyen bir sınavdır. Dolayısıyla unutulan bilgileri de hatırlatmakta fayda vardır. Bu bilgiler tabii ki ispatlanmış bilgilerdir. İspatlarını da talebiniz doğrultusunda video ile destekleyerek yapmayı düşünüyorum. Umarım faydalı olabilmişimdir, şunuda hatırlatmam gerekiyor parabolün kimi sorularında analitk geometri bilgisi gerekmekte. Bazı sorularda zorlanmışsanız analitik geometri bilginizin eksikliğinden kaynaklanıyor olabilir.
Youtube Kanalımızdan faydalanabilirsiniz.
Faydalı olması dileğiyle. Videoları YouTube platformu üzerinden daha rahat izleyebilirsiniz. Kanalı abone olup bildirimlerin tümünü açarsanız bu tarz içeriklerden ilk sizin haberiniz olur.


Büyük görsellerle devam edelim.




Abone ol : http://bit.ly/39cZQjM
⭐ Parabol : http://bit.ly/parabolac
⭐ Fonksiyonlar : http://bit.ly/fonksac
⭐ Matematik İspatlar : http://bit.ly/ispatac
⭐ Türev : http://bit.ly/turevac
⭐ İntegral : http://bit.ly/integralac
⭐ Trigonometri : http://bit.ly/trigoac
⭐ Karmaşık Sayılar : http://bit.ly/karmasikac
⭐ Logaritma : http://bit.ly/logaritmac
Kanalımızda yer alan tüm video ders notları tek sayfada.
Tüm PDF Notlar : https://ahmetcelen.com.tr/dersnot/
Kitaplar Halinde Çalışmalarım : https://fliphtml5.com/bookcase/snkwz
Fen Makaleleri : https://fenbilimleri.web.tr
Son terim – İlk terim / Artış Miktarı + 1 üzerinden bulunur.
Örneğin : 1+3+5+7+9 terim sayımız 5 kısa olduğu için sayabiliyoruz. Sağlamasını formülden yapalım.
Son terim : 9 , İlk terim 1 , Artış miktarı 2 (yani 2`şer 2şer artmış)
9-1/2+1 = 5 bulunmuş olur. (+1 formülden gelmiştir)