Tüm yazıları Ahmet Çelen

Parabol – Konu Anlatımlı PDF

Yazar: kategorisiAlan Yeterlilik Testi, Matematik Etiket , , , , , ,
Parabol Konu Anlatımlı Örnek Sorular PDF

Konu Anlatımlı Parabol PDF İndir

Nedir bu Parabol ?

İkinci dereceden fonksiyonların özelleştirilmiş isimleri Paraboldür.. Aynı zamanda müfredat olarak ikinci dereceden fonksiyon grafik uygulamaları diye de geçer. Parabol Konu Anlatımlı PDF başlığımızda konunun özetini sizlere PDF eşliğinde sunacağız. Her sene ÖSYM 1 tane parabol sorusu sormaktadır. Video çözümlü olarak sizlerde parabol için hazırladığımız fasikülü öğretmen veya öğrenci olarak incelemenizi tavsiye ederiz. İyi çalışmalar.

Aşağıdan isterseniz YouTube üzerinden video şeklinde müfredata uygun konu anlatımlarıma bakabilirsiniz. İstersenizde özet olarak makalemizi okumaya devam edebilirsiniz. Video konu anlatımları için tıklayın.

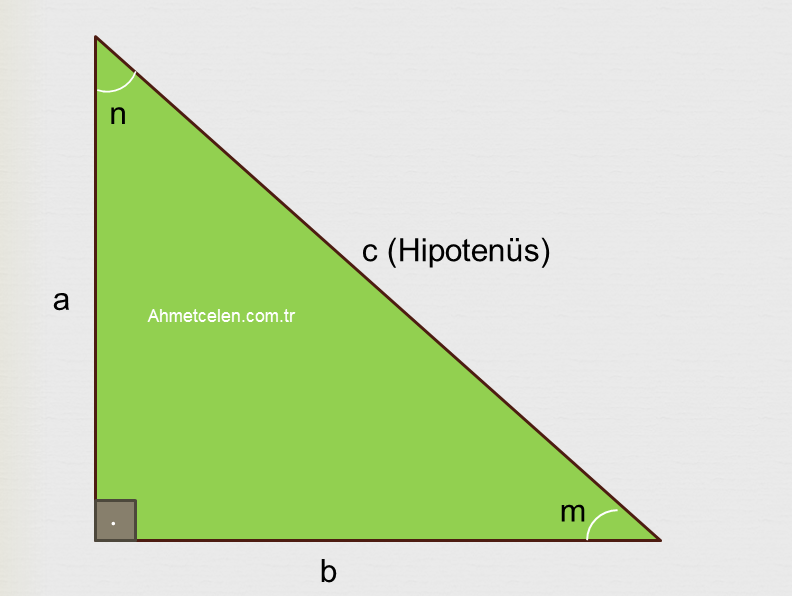
İkinci Derecede Denklemler Hatırlatmalar :

Parabol Tanım – Giriş

Parabol Tepe Noktası

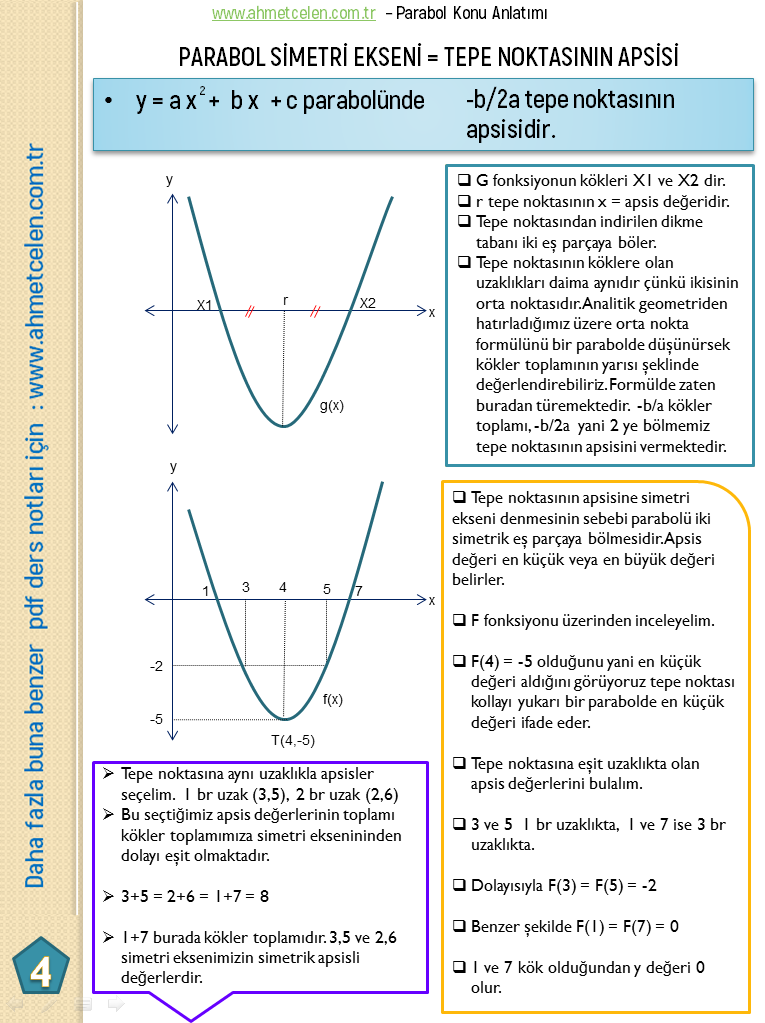
Bilinen verilerle denklem kurma :

Parabol sorularında genelde 2 farklı şekilde denklem yazmamız istenir.

  • Kökleri bilinen parabol
  • Tepe noktası bilinen parabol
  • Tabii bu veriler yeterli gelmeyecektir baş katsayıyı bilmediğimiz durumda parabol denklemini yazamayız. Grafik üzerinden parabolün üstünde olan bir noktanın koordinatları biliniyorsa denklemde yerine yazılarak baş katsayı da bulunabilir.

Delta – Parabol İlişkisi

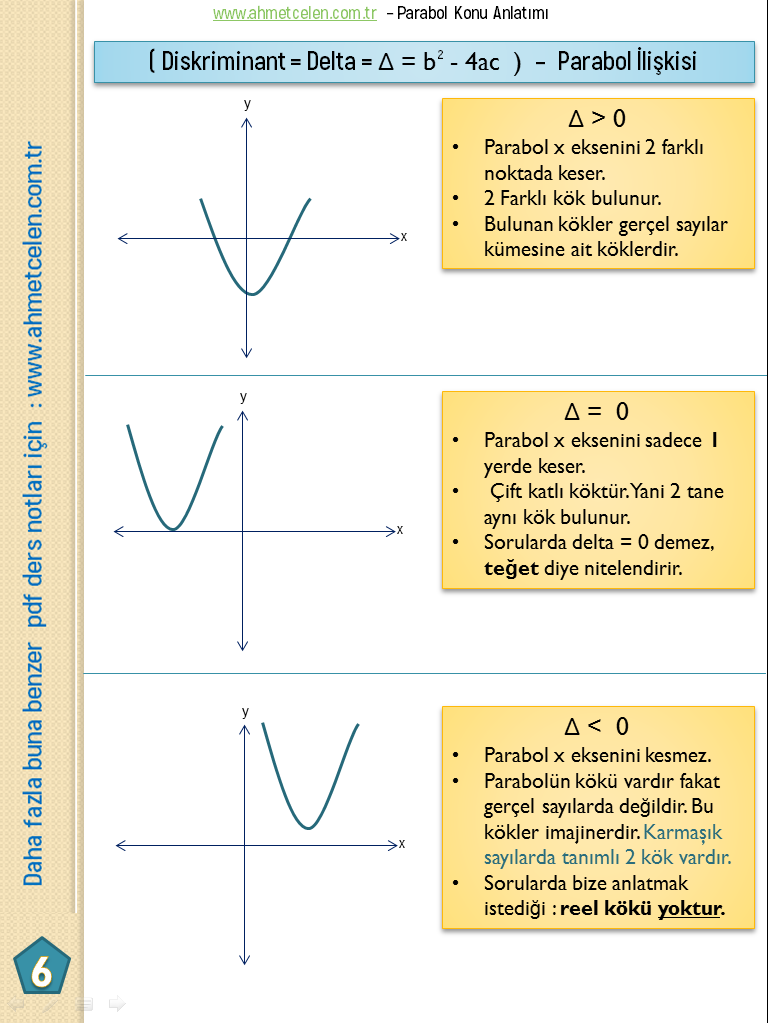
Parabol ile Doğru İlişkisi – Ortak Çözüm

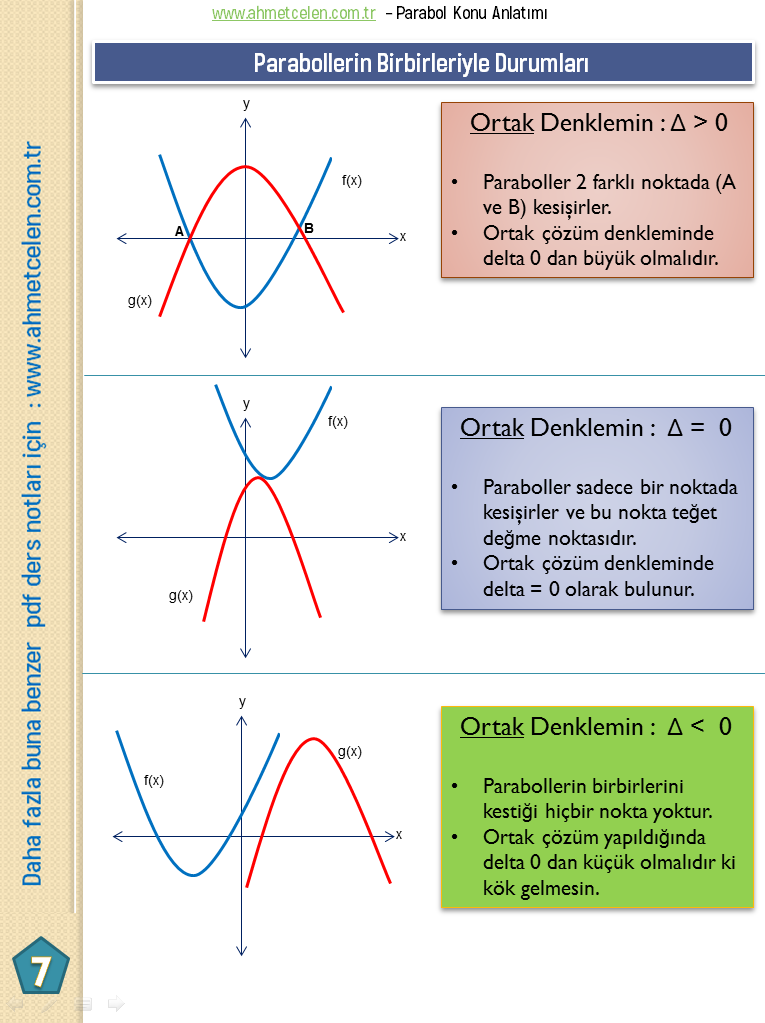
(Birbirlerine eşitleme) – Parabollerin birbirleriyle durumları

Arkadaşlar bu kısımda lütfen ezberden kaçının. Birbirlerini eşitleyerek denklem çözme olarak soru algınızı değiştirebilirsiniz. Doğru denklemleri konu anlatımdaki gibi olmayabilir – ise + diye geçer mesela o yüzden ezber değil denklem çözme mantığını kullanın burada bilmeniz gereken şey parabol ile doğru ortak çözüm yapılırken tüm ifadeler bir tarafta toplanır ve soruda verilenlere göre diskriminant incelemesi yapılır.


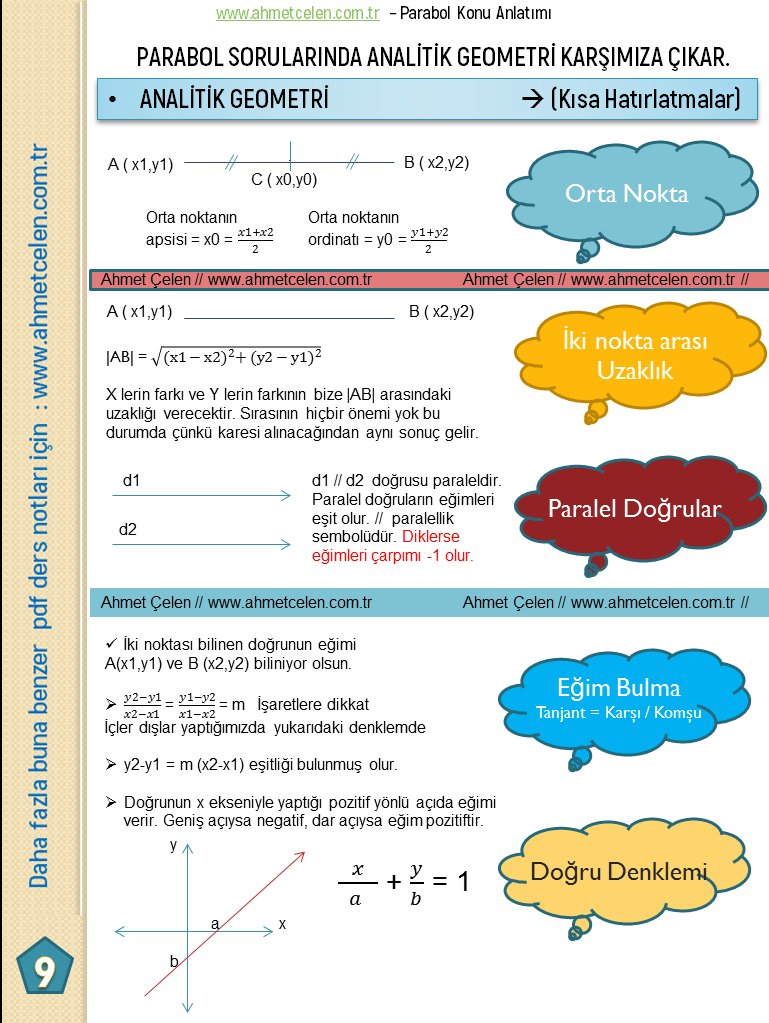
Parabol Soru Tüyoları (İşinize mutlaka yarayacak bilgiler)

PARABOL KONU ANLATIMI PDF – ALTIN TÜYOLAR

Lise son sınıfsanız eğer türev-parabol ilişkisini incelemenizi öneririz.

Her kaynakta hemen hemen yer verilmeyen bazı unutulan bilgileride ekleme gereği duyduk. Alan Yeterlilik Testi bilgi isteyen bir sınavdır. Dolayısıyla unutulan bilgileri de hatırlatmakta fayda vardır. Bu bilgiler tabii ki ispatlanmış bilgilerdir. İspatlarını da talebiniz doğrultusunda video ile destekleyerek yapmayı düşünüyorum. Umarım faydalı olabilmişimdir, şunuda hatırlatmam gerekiyor parabolün kimi sorularında analitk geometri bilgisi gerekmekte. Bazı sorularda zorlanmışsanız analitik geometri bilginizin eksikliğinden kaynaklanıyor olabilir.

Eksikler ve bağlantıları nelerdir?

  • Önce eksiklerimizi tespit etmeliyiz.
  • Eksik olduğumuz konuyu gördüğümüzde üstüne düşmeli ve ispatlarına kadar bu konuyu anlamamız gerekiyor.
  • Örneğin çarpanlarına ayırma konusu matematiğin her kısmında karşınıza çıkabilir dolayısıyla bunda kesinlikle eksiğiniz olmamalı.
  • Onun haricinde matematikte fonksiyon altyapısı da bir hayli önem taşımakta.
  • İlave olarak doğru ve parabol sorularında eğim gibi kavramlar devreye girmektedir. Bu kavramları yan yana duyduğumuzda analitik geometri bize gülümsüyor.
  • Matematik sarmal yapıya sahiptir. Bu sarmal yapıda eksiğinizin olmaması sizin konuları ve soruları iyice kavramanızda çok büyük bir faktör olarak rol oynayacaktır.

Youtube Kanalımızdan faydalanabilirsiniz.

ahmet çelen youtube

Faydalı olması dileğiyle. Videoları YouTube platformu üzerinden daha rahat izleyebilirsiniz. Kanalı abone olup bildirimlerin tümünü açarsanız bu tarz içeriklerden ilk sizin haberiniz olur.

Toplam fark ve Yarım Açı Formülleri Trigonometri

Yazar: kategorisiAlan Yeterlilik Testi, Geometri, Matematik Etiket , , , , ,
trigonometri

Büyük görsellerle devam edelim.

Sinus formülleri
  • Diğer içeriklerimiz ve konu anlatımlarımız :

Abone ol : http://bit.ly/39cZQjM​

⭐ Parabol : http://bit.ly/parabolac
⭐ Fonksiyonlar : http://bit.ly/fonksac
⭐ Matematik İspatlar : http://bit.ly/ispatac
⭐ Türev : http://bit.ly/turevac
⭐ İntegral : http://bit.ly/integralac
⭐ Trigonometri : http://bit.ly/trigoac
⭐ Karmaşık Sayılar : http://bit.ly/karmasikac
⭐ Logaritma : http://bit.ly/logaritmac

Kanalımızda yer alan tüm video ders notları tek sayfada.

Tüm PDF Notlar : https://ahmetcelen.com.tr/dersnot/

Kitaplar Halinde Çalışmalarım : https://fliphtml5.com/bookcase/snkwz

Fen Makaleleri : https://fenbilimleri.web.tr

Tam soy ve yarı soy metaller

Yazar: kategorisiAlan Yeterlilik Testi, Kimya, Temel Yeterlilik Testi Etiket , , , ,

Tam Soy Metaller : Altın , Platin

  • Elektriği çok iyi iletirler.
  • Aşınma ve yükseltgenme direnci çok yüksek olan metallerdir.
  • Çoğunlukla parlak görünüşe sahiptirler.
  • Doğada fazla bulunmazlar.
  • Kral suyu ile tepkimeye girebilirler.
  • Altın (Au), Platin (Pt) tam soy metallere örnektir.

Yarı Soy Metaller : Civa , Gümüş , Bakır

  • HNO3 ve H2SO4 ile tepkimeye girerler.
  • Havanın oksijeni den etkilenirler, tepkimeye genellikle oksijen içeren kuvvetli asit ve bazlarla girerler.
  • Kuvvetli asit veya baz %100 iyonlarına ayrışan demektir.
  • Hg (Civa) , Cu (Bakır) , Gümüş (Ag) yarı soy metallerdendir.

Kodlama / Şifreleme kolay ezberleme taktiği olarak :

Cumhur Hak(g)sızca Ağ(g)layanları Avucunda Patlatır. diyerek kodlayabilirsiniz.

Araştırmalar sonucu elde edilen bilgilerdir, düzeltme gereken kısımları bildirebilirsiniz. bilgi@ahmetcelen.com.tr

Trigonometrik Fonksiyonlar

Yazar: kategorisiAlan Yeterlilik Testi, Geometri, Matematik, Temel Yeterlilik Testi Etiket , , , , , , ,

Sinus fonksiyonu

  • Sinus fonksiyonu dik üçgenlerde karşı/hipotenüs ile bulunur.
  • Birim çember koordinat sisteminde ordinat eksenini olarak geçer.
  • Sinus teoremi ile kenar uzunlukları oran ile bulunabilir.
  • Sinusle açı biliniyorsa alan bulunabilir.

Kosinus Fonksiyonu

  • Kosinus fonksiyonu dik üçgenlerde komşu/hipotenüs ile bulunur.
  • Birim çember üzerinde koordinat sisteminde apsis ekseni olarak geçer.
  • 2 kenarı bilinen ve bilinmeyen kenarın baktığı açı bilinen üçgende kosinus teoremi uygulanarak kenar uzunluğu bulunabilir.

Tanjant Fonksiyonu

  • Tanjant fonksiyonu dik üçgenlerde karşı/komşu ile bulunur.
  • Birim çemberde y eksenine paralel x=1 ve doğrusudur.
  • Tanjant fonksiyonu eğim ve türev ile çok ilişkilidir.
  • Tanjant fonksiyonu bir doğrunun x ekseni ile yaptığı pozitif yönlü açıyı (eğimi) ifade eder.

Kotanjant Fonksiyonu

  • Kotanjant fonksiyonu dik üçgende komşu/karşı ile bulunur.
  • Birim çemberde x eksenine paralel y=1 doğrusudur.

Kosekant Fonksiyonu (cosec)

  • 1/sinus bağıntısına eşittir.

Sekant Fonksiyonu ( sec )

  • 1/kosinus bağıntısına eşittir.

Dik üçgende trigonometrik oranlar

Yukarıdaki görseldeki üçgene göre trigonometrik oranlar :

sin m = a/c —> (karşı/hipotenüs) – m açısına göre

cos m = b/c —> (komşu/hipotenüs) – m açısına göre

tan m = a/b —> (karşı/komşu) – m açısına göre

cot m = b/a —> (komşu/karşı) – m açısına göre

1`den n`e kadar olan sayıların toplam formülü – Gauss Toplamı

Yazar: kategorisiAlan Yeterlilik Testi, Matematik, Temel Yeterlilik Testi Etiket , ,

1 den n`e kadar olan sayıları toplamak istersek aşağıdaki Gauss Formülünü kullanabiliriz.

n . (n+1) / 2

Örneğin 1+2+3+4+5+6+7 toplamını bulalım.

7 . (7+1) / 2 den = 28 olarak bulunmuş olunur.

Eğer başka bir sayıdan başlatılmış ise 1 den n`e kadar olan sayıların toplamını bulup, baştan olmayan toplamları çıkarıp sonuca ulaşabiliriz.

Örneğin : 4+5+6+7+8

1 den 8`e kadar olan sayıların toplamını bulalım.

8.9/2 = 36 yaptı. 1 den 3`e kadar olan sayıların toplamını çıkarmalıyız çünkü istenilen ifadede yoklar. 3.4/2 = 6

İşlemimizin sonucu 36-6 = 30 bulunmuş olur.

Soygazlar – Asalgazlar Özellikleri

Yazar: kategorisiAlan Yeterlilik Testi, Kimya, Temel Yeterlilik Testi Etiket
8A Grubu

Soygazlar, diğer isimleriyle “asalgazlar”, kendini elektron sayısı olarak oktete(8) ve dublete (2) tamamlamış elementlerdir. Soygazların elektronegatiflik ve elektron ilgileri yoktur. 

Soygazlarda Helyum (He) elementi son yörüngesinde 2 elektron bulunmaktadır. Bu iki element harici tüm soygazların son yörüngesinde 8 elektron bulunmaktadır.

Soygazların Özellikleri :

  • Doğada element halinde bulunurlar.
  • Oda koşullarında gaz halinde bulunurlar.
  • Kararlı yapıya sahiptirler.
  • Saydam (ışığı geçiren) bir yapıya sahiptirler.
  • Erime ve kaynama noktaları düşük elementlerdir.
  • Herhangi bir reaksiyona girmedikleri istekleri çok azdır, bileşik oluşturmazlar.
  • Isı ve elektriği iletmezler.
  • 8A baş element grubunda yer alırlar.
  • Renksizdirler.
  • Tek atomlu yani monoatomiktirler.
  • Helyum (He) ve Radon (Rn) dışındakiler havada bulunurlar.

Soygaz Elementlere Örnekler :

  • Helyum – He
  • Neon – Ne
  • Argon – Ar
  • Kripton – Kr
  • Ksenon – Xe
  • Radon – Rn