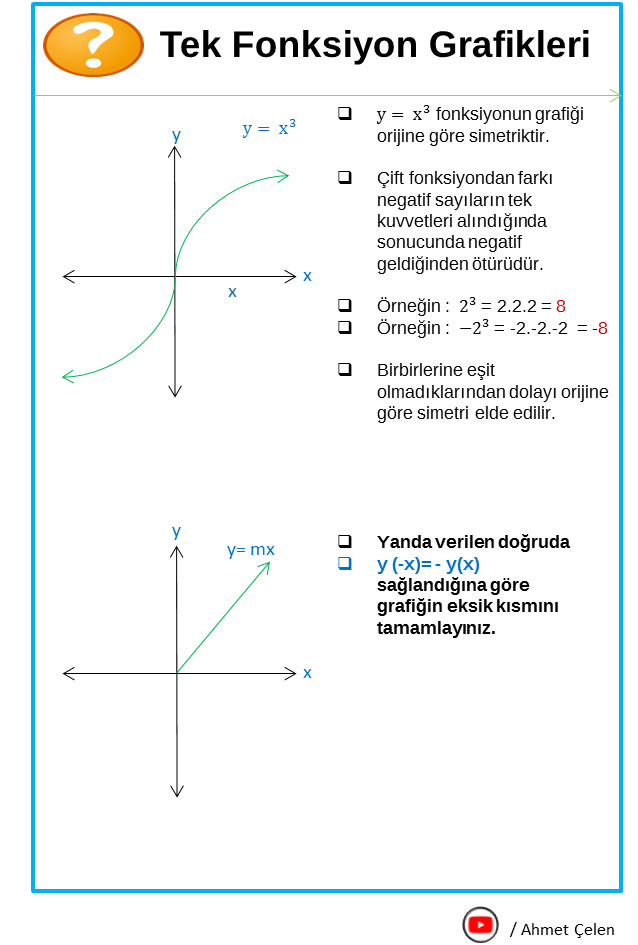
Tek Fonksiyonlar :
- f(-x) = – f(x) eşitliğini sağlarlar. (- yi dışarı kusarlar)
- Tek fonksiyonların grafikleri orijine göre simetriktir.
- Tek fonksiyonda çift dereceli terim bulunmaz.
- Örneğin : X3 ve X5 tek fonksiyondur.
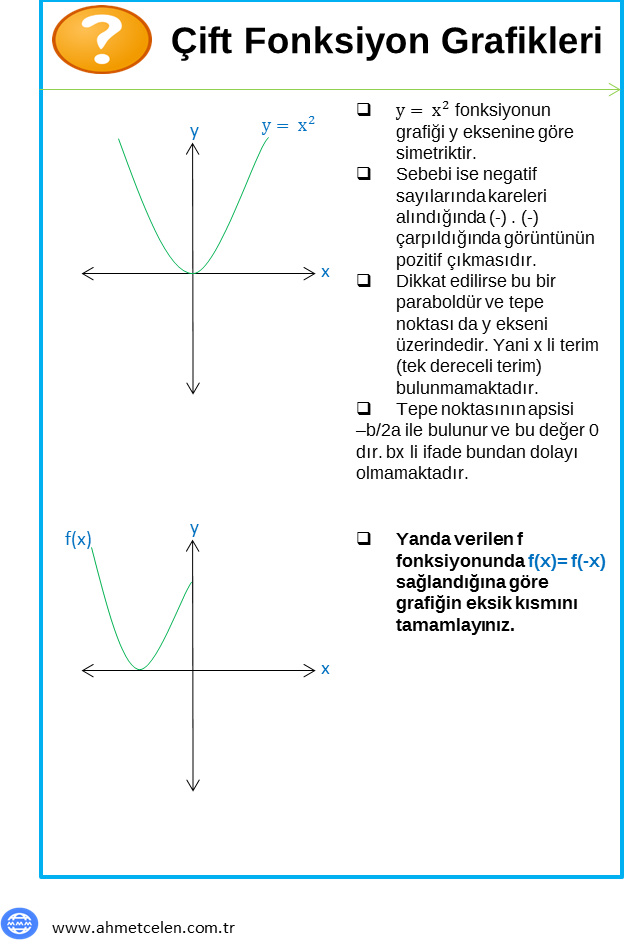
Çift Fonksiyonlar :
- f(-x) = f(x) eşitliğini sağlarlar. ( – yi yutarlar)
- Çift fonksiyonların grafikleri y eksenine göre simetriktir.
- Çift fonksiyonlarda tek dereceli terim bulunmaz.
- Örneğin : X2 parabolü çift fonksiyondur.
Tek ve Çift Fonksiyonlar Konu Anlatımı PDF olarak ücretsiz bir şekilde sizlere sunacağız. Aşağıda kırmızı bağlantıya tıklayarak indirebilirsiniz.
Faydalı olmasını diliyorum. ~ Ahmet ÇELEN
Ayrıntılı inceleyelim :
Yukarıda çift ve tek fonksiyonların özetini kısaca aktardık biraz detay bilgi isteyenler için görseller yardımıyla değerlendirelim.
DERECE Kavramı :

Derece Kavramı Örneği :

ÇİFT Fonksiyonlar ve Özellikleri :

Çift Fonksiyonların Grafikleri :
TEK FONKSİYONLAR

TEK FONKSİYONLARIN GRAFİKLERİ
ÖNEMLİ UYARILAR :
- Bir fonksiyonda tek ve çift dereceli terim aynı anda bulunuyorsa bu fonksiyon ne tek ne çift fonksiyondur.
- h(x) = 0 fonksiyonu hem tek hem çift fonksiyondur. Sebebiyse grafiğinin hem orijine hemde y eksenine simetrik olmasıdır.

TEK VE ÇİFT FONKSİYONLARDA BİLEŞKE

Birebir ve Örten Durumları Hatırlatması

Tek ve Çift Fonksiyonlar Örnek Sorular
Örnek Soruların Çözümü ve cevapları
Arkadaşlar bu soruların çözümlerini video olacak şekilde YouTube kanalımda çözdüm. Aşağıdan soruların çözümü ve genel olarak videolu konu anlatımı izleyebilirsiniz. Videoyu yazıma aşağıya entegre edeceğim.
Tek ve Çift ve Tüm Fonksiyonlar
Fonksiyonlar matematiğin yapı taşıdır. En temel bilgiler ve diğer konuların temelidir. Fonksiyonları bu sebeple çok sağlam tutmalıyız. İlerleyen konularda limit türev integral gibi ağır konularda fonksiyon temelimiz iyi olursa zorluk çekmeyiz. Ayrıca bazı özel fonksiyonların grafiklerini çizebilmemiz ve nasıl olduğunu bilmemizde büyük kolaylık sağlar.
X2 , X3kök içerisinde x , In x gibi karşımıza çok çıkacak fonksiyonların grafiklerini bilirsek eşitsizlik ve kök (kaç noktada kesişir) gibi sorularında grafikten hiç işlem yapılmaksızın tespit edilebilir ve cevaba ulaşmış oluruz. Özet olarak fonksiyonlar hem TYT hem AYT matematik için büyük önem taşımaktadır. Ayrıca çarpanlara ayırma da matematiğin temelidir ikisini iyi bilirseniz sorularda her konuda olursa olsun çok zorlanmazsınız.